Measuring is the Foundation
Measurement strategies are essential to understanding how number lines work. These strategies allow students to build number lines from scratch and to interpret and extend existing number line diagrams. In addition, they are required to make sense of more sophisticated number line strategies such as:
- Split distances to label number lines.
- Apply base-ten concepts to label number lines.
- Estimate locations of points on number lines.
As we investigate these more advanced strategies in future posts, basic measurement strategies will be applied to justify why these new strategies work.
Characteristics of Fluency Pyramids
The fluency pyramid above helps demonstrate a few of the important characteristics of fluency pyramids in general:
- Address Overlooked Concepts and Strategies
- Build a Solid Foundation to Support Future Learning
- Solve Problems With a New Relationship
- Solve a Variety of Problem Types
- Build on Previous Concepts and Skills
Each of these characteristics is explained in more detail below.
Address Overlooked Concepts and Strategies
The concepts and strategies at the base of fluency pyramid are often overlooked because many adults take them for granted. For number lines, many educators look at a number line, scale, or axis and recognize that distance represents a value. For many students, this relationship is not obvious and needs to be taught and practiced. And, as explained below, the base strategy should be revisited to justify more sophisticated strategies as they are introduced.
Build a Solid Foundation to Support Future Learning
Students need many opportunities to explore, practice, and apply the foundational concepts and strategies in a fluency pyramid. That is why the visual representation in the pyramid is built wide and supports the more advanced layers above. In addition, concepts and strategies at the base of a fluency pyramid will often be required to make sense of the more advanced and formal strategies at the top of the pyramid.
For example, the split distances strategy allows students to partition an interval, such as 200 to 300, into 5 equal parts by dividing the distance of 100 by 5. The tick marks separating the five equal parts can now be labeled as 220, 240, 260, and 280. In addition, students can now easily estimate the value of points between these tick marks.
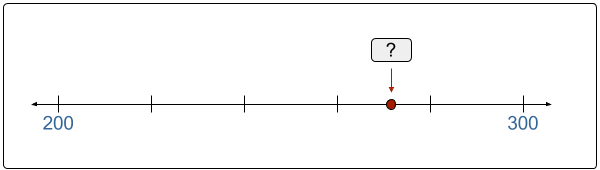
Note that the split distances and estimation strategies are applications of the basic measurement strategy. This is because measuring is required to justify the labeling of equally spaced tick marks and the estimation of points between them. When students are proficient with a foundational strategy, they are likely to see these more sophisticated problems as just more advanced versions of a basic problem that they are already very familiar with. This connection helps with understanding, efficiency, and retention. In future posts, we will investigate these more sophisticated number line strategies.
Solve Problems With a New Relationship
The foundation of a fluency pyramid usually involves students learning and applying an informal strategy or concept to solve a set of new problem types. In the case of number lines, the informal concept is to use a scale, or measurement standard, to build, label, and extend number lines. This informal concept defines how number lines are different from the simple ordering of whole numbers. That is, the distances between different points on a number line represent values. This is a new and powerful relationship for students to practice and apply.
Solve a Variety of Problem Types
Foundational concepts or strategies usually allow students to solve a variety of problem types with differing degrees of difficulty. From an instructional strategy perspective, this allows teachers to offer a mix of problem types that are all solvable for students using the newly learned strategy. This problem-solving approach challenges students to figure out how to use the new strategy to answer the novel problem types and not by mimicking a specific procedure to get a right answer. This also allows teachers to challenge students to explain and justify their own solutions instead of just listing the steps that they followed to get their answer.
Build on Previous Concepts and Skills
The foundation of one fluency pyramid is built on top of the knowledge, concepts, and skills that students have previously learned. For example, the basic measurement strategy requires students to apply basic counting, ordering, addition, and subtraction skills. The critical point here is that students with those basic understandings are ready to be introduced to measurement strategies and to start using them to solve problems with number lines.