Tasks and Problems for Younger Students

The fluency pyramid in the previous post was developed for middle school math teachers that are looking to review number line strategies with their students. Because the pyramid was built with a middle school perspective, the base of the pyramid condenses a number of problem types, strategies, and concepts into one level of the pyramid. Below is a more expansive sequence of problems that would be appropriate for grades 2 and 3.

• Build Number Lines with Snap Cubes and Measure from Zero to Points
• Build Number Lines with Cuisenaire Rods or Paper Strips and Measure from Zero to Points
• Label and Extend Existing Number Lines to 50, 100, 200, and 1,000

 

Review Problems – Basic Measurement Strategies

Directly below are few different problem types that can help teachers review the basic measurement strategy in middle school. In each problem, bars or tick marks mark off equal distances. Students then use the equal distances and existing values on the line to label other points and tick marks. Note, for the last problem, it is important to challenge students to justify their answer with a measurement strategy—this will require halving the first interval on the line.

 

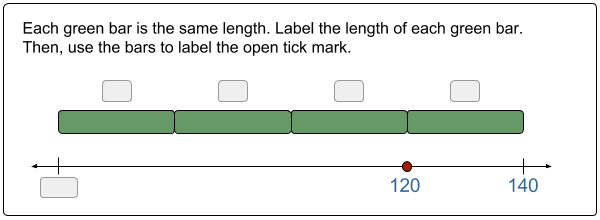
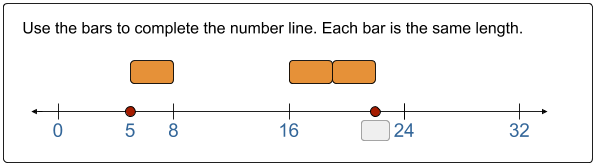
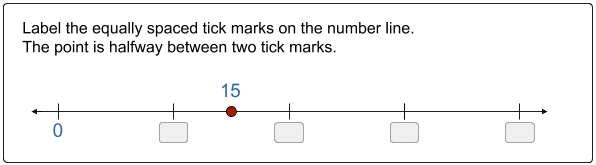
Apply Problems – Basic Measurement Strategies

Because diagrams with linear scales show up everywhere in grades 6-8, a review of number line concepts can help students master on-grade-level content. The example below is very similar to the initial number line problem that was discussed in this series of blog posts. Students that are familiar with solving the more basic number line problem will be better prepared to complete this percent bar and make sense of this problem type. Below is an example of one such problem. Additional examples of middle school application problems will be given as more advanced number line strategies are investigated.

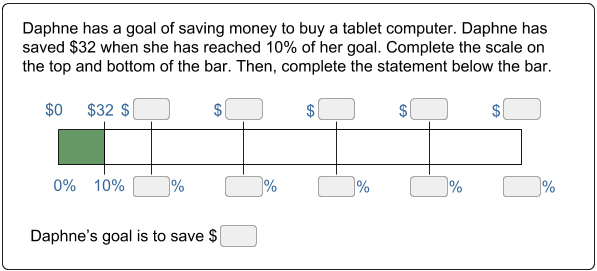
It is also important to note that, in the problem above, students use a second- or third-grade strategy to solve and to better understand a sixth-grade concept. This is why building fluency matters. Foundational concepts and strategies often have applications well beyond their initial context and provide entry points for learning new mathematics.