Tasks and Problems for Younger Students

The fluency pyramid in the previous post was developed for middle school math teachers that are looking to review number line strategies with their students. Because the pyramid was built with a middle school perspective, the base of the pyramid condenses a number of problem types, strategies, and concepts into one level of the pyramid. Below is a more expansive sequence of problems that would be appropriate for grades 2 and 3.

• Build Number Lines with Snap Cubes and Measure from Zero to Points
• Build Number Lines with Cuisenaire Rods or Paper Strips and Measure from Zero to Points
• Label and Extend Existing Number Lines to 50, 100, 200, and 1,000

 

Review Problems – Basic Measurement Strategies

Directly below are few different problem types that can help teachers review the basic measurement strategy in middle school. In each problem, bars or tick marks mark off equal distances. Students then use the equal distances and existing values on the line to label other points and tick marks. Note, for the last problem, it is important to challenge students to justify their answer with a measurement strategy—this will require halving the first interval on the line.

 

Apply Problems – Basic Measurement Strategies

Because diagrams with linear scales show up everywhere in grades 6-8, a review of number line concepts can help students master on-grade-level content. The example below is very similar to the initial number line problem that was discussed in this series of blog posts. Students that are familiar with solving the more basic number line problem will be better prepared to complete this percent bar and make sense of this problem type. Below is an example of one such problem. Additional examples of middle school application problems will be given as more advanced number line strategies are investigated.

It is also important to note that, in the problem above, students use a second- or third-grade strategy to solve and to better understand a sixth-grade concept. This is why building fluency matters. Foundational concepts and strategies often have applications well beyond their initial context and provide entry points for learning new mathematics.

Measuring is the Foundation

Measurement strategies are essential to understanding how number lines work. These strategies allow students to build number lines from scratch and to interpret and extend existing number line diagrams. In addition, they are required to make sense of more sophisticated number line strategies such as:

• Split distances to label number lines.
• Apply base-ten concepts to label number lines.
• Estimate locations of points on number lines.

As we investigate these more advanced strategies in future posts, basic measurement strategies will be applied to justify why these new strategies work.

Characteristics of Fluency Pyramids

The fluency pyramid above helps demonstrate a few of the important characteristics of fluency pyramids in general:

• Address Overlooked Concepts and Strategies
• Build a Solid Foundation to Support Future Learning
• Solve Problems With a New Relationship
• Solve a Variety of Problem Types
• Build on Previous Concepts and Skills

Each of these characteristics is explained in more detail below.

 

Address Overlooked Concepts and Strategies

The concepts and strategies at the base of fluency pyramid are often overlooked because many adults take them for granted. For number lines, many educators look at a number line, scale, or axis and recognize that distance represents a value. For many students, this relationship is not obvious and needs to be taught and practiced. And, as explained below, the base strategy should be revisited to justify more sophisticated strategies as they are introduced.

 

Build a Solid Foundation to Support Future Learning

Students need many opportunities to explore, practice, and apply the foundational concepts and strategies in a fluency pyramid. That is why the visual representation in the pyramid is built wide and supports the more advanced layers above. In addition, concepts and strategies at the base of a fluency pyramid will often be required to make sense of the more advanced and formal strategies at the top of the pyramid.

For example, the split distances strategy allows students to partition an interval, such as 200 to 300, into 5 equal parts by dividing the distance of 100 by 5. The tick marks separating the five equal parts can now be labeled as 220, 240, 260, and 280. In addition, students can now easily estimate the value of points between these tick marks.

Note that the split distances and estimation strategies are applications of the basic measurement strategy. This is because measuring is required to justify the labeling of equally spaced tick marks and the estimation of points between them. When students are proficient with a foundational strategy, they are likely to see these more sophisticated problems as just more advanced versions of a basic problem that they are already very familiar with. This connection helps with understanding, efficiency, and retention. In future posts, we will investigate these more sophisticated number line strategies.

 

Solve Problems With a New Relationship

The foundation of a fluency pyramid usually involves students learning and applying an informal strategy or concept to solve a set of new problem types. In the case of number lines, the informal concept is to use a scale, or measurement standard, to build, label, and extend number lines. This informal concept defines how number lines are different from the simple ordering of whole numbers. That is, the distances between different points on a number line represent values. This is a new and powerful relationship for students to practice and apply.

 

Solve a Variety of Problem Types

Foundational concepts or strategies usually allow students to solve a variety of problem types with differing degrees of difficulty. From an instructional strategy perspective, this allows teachers to offer a mix of problem types that are all solvable for students using the newly learned strategy. This problem-solving approach challenges students to figure out how to use the new strategy to answer the novel problem types and not by mimicking a specific procedure to get a right answer. This also allows teachers to challenge students to explain and justify their own solutions instead of just listing the steps that they followed to get their answer.

 

Build on Previous Concepts and Skills

The foundation of one fluency pyramid is built on top of the knowledge, concepts, and skills that students have previously learned. For example, the basic measurement strategy requires students to apply basic counting, ordering, addition, and subtraction skills. The critical point here is that students with those basic understandings are ready to be introduced to measurement strategies and to start using them to solve problems with number lines.

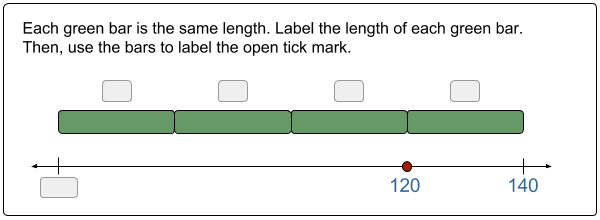
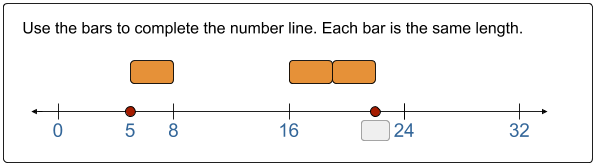
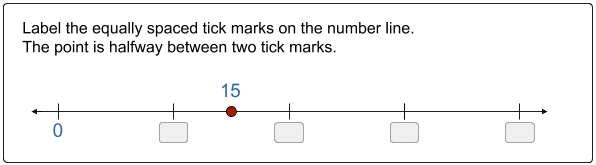
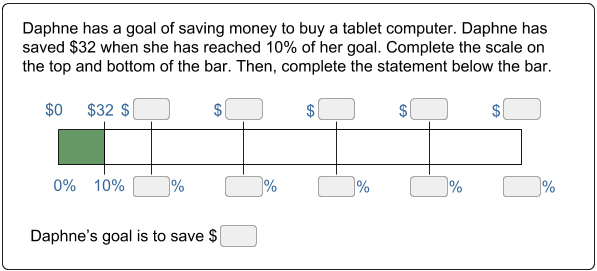
Easier Said than Done

As math educators, we have a definition for a number line floating around in our heads. So, for the heck of it, write down that definition. Then, keep reading.

Next, you might want to Google “definition of a number line” and see what comes up. Go and read four or five different definitions. What do you notice? Yeah, nobody’s definition is the same!

Looking through the various results, you will recognize that the definition changes based on the intended audience of the page that you are viewing. For example, Merriam-Webster gives two definitions, one formal definition, which is pretty good for a high school math class, and one for “Students” which is almost useless. Webster’s New World College Dictionary gives a completely different definition, and that definition has significant mathematical issues. The American Heritage Dictionary of the English Language also has a good definition for high school students.

The definitions get worse when you look at free math websites. On one site, which will remain nameless, the definition states that numbers are placed in the “correct position” on a line, with no details on how the correct position is determined. The video on that site does a much better job because it uses a measurement strategy to build a number line representation. Unfortunately, in an attempt to use a tool that is familiar to students, Legos, the video misrepresents two important number line characteristics, tick marks and the intervals between them. More specifically, the thickness of each tick mark in the video is equal to the space between each set of tick marks. This confuses an otherwise valuable demonstration of a measurement strategy.

So why does any of this matter?

My first point is that coming up with a good definition of a number line is hard and that a good definition has to be appropriate for the grade level that you are teaching.

My second point is that a good definition for younger students requires a clear description or demonstration of how distances are measured on a number line.

Expanding on this last point, even good definitions for number lines are rendered meaningless unless a student has a proficient understanding of the basic measurement strategy, which was investigated in previous posts. The idea that a particular distance on a number line corresponds to a particular value is essential to making sense of how number lines work. That’s why this blog spent three posts investigating this fundamental concept.

If we take into account the fact that a fair number of students in grade 3 and above are weak, at best, with measurement strategies, there is a high likelihood that the definitions that we give and the number line problems that we offer in math class are going right over some students’ heads. Students can memorize a definition till they can say it in their sleep, but if they do not understand and cannot apply the basic measurement strategy, any definition of a number line is pretty useless. For these students, number line definitions end up sounding like what Charlie Brown’s teacher says, “Wah wa-waah, wah … .”

 

Characteristics of Number Lines

Instead of coming up with a one or two sentence definition, I’m inclined to list the set of characteristics that define a number line. This approach has the benefit of emphasizing the critical concepts and conventions that go into understanding this common representation. It also allows math educators to introduce refinements to the definition as students knowledge of number types expands to fractions, decimals, integers, rational numbers, and irrational numbers (and, for you high school folks, real and imaginary numbers).

The two lists below lay out the characteristics of number lines with whole numbers for grade 3 and above. Note that the lists are currently written for teachers. Based on feedback from readers, I will refine this list so that it is also appropriate for students.

Concepts – Number Lines with Whole Numbers

• Each number line has a scale (whether it is shown or not) that is used to measure distance on that line.
• The value of a point (representing a whole number) on a number line is the measured distance between zero and that point.
• The measured distance between two points on a number line is the difference of the two numbers represented by the points.
• A measured distance on one part of a number line represents the same value if it is moved to some other place on that number line.
• Number lines that do not include a point for zero can be extended to the left to include zero.
• The scales on different number lines can be the same or different. If the scales on two number lines are the same, measurements on one line can be used as measurements on the other line.

Conventions – Number Line with Whole Numbers

• Whole number values increase from left to right on a number line.
• Tick marks on number lines are labeled just like points (they represent the distance from 0).
• Tick marks are often used to mark off equal distances on a number line.
• The distance between points is measured from the center of each point.

When you look at all the concepts and conventions that go into a basic number line for whole numbers, it becomes clear that students need lots of opportunities to build, extend, and label these diagrams. It’s also not surprising that many students struggle with these representations precisely because their work with them has been so superficial.

Split a Measurement in Half

An extension of the basic measurement strategy involves another basic mathematical concept, splitting something in half to get two equal parts.

Fortunately, most students come to school with this concept. Why, because most students have been in the situation where they and someone else want to share something and “you can’t have more than me.” So what do they do, they split the shared item into two equal parts.

Students can combine the halving and measurement strategies to halve even-valued distances on a number line. To start with, students can fold a bar (strip of paper) representing 4 in half. When the bar is unfolded, there are two equal parts. Students can then show that a bar of length 2 plus a bar of length 2 is equal to a bar of length 4. These steps can then be repeated to halve a bar of length 2 to get a bar of length 1.

It’s important to note that this halving technique applies the basic measurement strategy to justify the length of two equal parts that are created. One way to challenge students is to ask them if it would be okay to label one of the equal parts 1 and the other equal part 3. The point here is to emphasize a fundamental rule that governs how a number line works: two distances that measure the same length on a given number line have to be represented by the same number.

 

Measure to Locate Points

The bars of length 4, 2 and 1 can now be used to locate points on a number line that is marked off in intervals of 4.

The strategy demonstrated in the animation uses a given measurement to add or subtract from existing points on a number line. After the fact, the results are double-checked by using the given measurements to show that the distance from 0 is correct. For younger or less experienced students, you may want to build the distance from 0 first and then show that the distances from existing points are also correct.

 

Common Placement Errors

Students with a weak understanding of number lines often do not use measurement strategies when locating points on a number line. For example, to locate 2 on a number line with intervals of 4, these students move “just to the right” of 0 and make a point for 1. Then, they will move a little farther to the right and make a point for 2. In this case, the placement of the point for 2 is based on being a little more than 0 and ignores the placement of the tick mark for 4. A basic measurement strategy can be used to challenge this incorrect strategy by measuring the distance between 0 and 2 and then showing that a distance of 2 + 2 on the line does not line up with 4.

A similar misconception may be masked by students stating that “2 is between 0 and 4” and not clearly stating that it is halfway between. Be sure to push back when a student gives this response. For example, purposely misinterpret their directions by placing the point for 2 clearly closer to 0 or 4. Students that meant halfway will quickly restate their directions. For students that don’t object, more work with the basic measurement strategy is needed.

Number Line with Intervals of 1

The basic measurement strategy introduced in the previous post can be used to build a number line from scratch.

Below is a set of directions for building a line with intervals of 1.

1. Getting started requires a blank number line and a standard unit of measure. Let’s say a bar or a rectangular strip of paper.
2. Decide what number is represented by the length of the bar. Let’s say that the bar represents a length of 1.
3. Draw a tick mark near the left end of the line and label it 0.
4. Line up the left end of the bar to the right of the 0 tick mark and measure off a distance of 1 by making a tick mark at the right end of the bar. Because 0 + 1 is 1, label the new tick mark with a 1.
5. Slide the bar just to the right of the tick mark for 1 and then make a new tick mark for 2.
6. Repeat to measure tick marks for 3, 4, 5, and so on.

 

Intervals Other than 1

The process above can be repeated with the initial length of the bar set to a number other than one. If that number is 4, then the next five tick marks would be labeled 4, 8, 12, 16, and 20.

Naturally, the next question might be, “Where would we locate 2, 1, or 7 on this line?” To locate these points, the bar of length 4 could be folded in half to measure 2 and that length could be folded in half to measure 1. A more formal version of this “splitting” strategy will be investigated in a series of future posts. But note that justifying why the halving strategy works requires invoking the basic measurement strategy.

 

Start Somewhere Other than 0

The process above can be repeated with a start point of 500 and an initial length of 20. The tick marks on this number line will be labeled 500, 520, 540, 560, 580, and 600.

 

Why Make Students Build Number Lines from Scratch?

Good question. If you want, try it with a set of your students and see how it goes. Then ask yourself, what questions would you or your students ask. For example, on the number line that starts with 500, “Where would zero go?”.

So, instead of me spouting off on this question, head over to the comments section and tell us what you think or what you found when you tried out this task with students. In the next post, I will pull together what we’ve come up with.

 

Make Students Measure

Students do not need a fancy animated bar to apply the strategy that is demonstrated in the video above. In fact, most math teachers (or proficient students) would “eye ball” the solution to this problem.

But, for students that demonstrate a weak understanding of this strategy, it is essential for them to use some tool to measure. If they are working on a printed page, they can use the edge of a piece of paper to mark-off and slide their measurements. If they are presenting their reasoning at an interactive whiteboard, they might use their hands, fingers, or a movable drawing on the board to solve the problem.

Why make students measure to solve problems like this? Because physically measuring distances on a number line reinforces a fundamental concept of number lines:

The relative positions of tick marks and points on a number line
hold important information.

Students that lack this fundamental concept will often ignore the essential information that a number line or diagram is presenting. And, since diagrams with linear scales show up everywhere in mathematics, students that are not fluent with basic measurement strategies will repeatedly run into issues when solving problems that include them.

Since this measurement technique will form the basis for more sophisticated number line strategies, students should get many opportunities to apply the technique and use it to justify their solutions. See the PDF links below for additional practice and apply opportunities for students.

Now, can practicing these measurement strategies be taken too far? For students that demonstrate proficiency with the strategy, the answer is yes. But, even a proficient student should be expected to apply the strategy to justify their reasoning when solving more advanced problems.

 

Practicing Measurement Strategies

Below is a 4-page lesson on measuring to label number lines. The Explore page can be used review or reteach the basic measurement strategy. The Practice page is self-explanatory. The Apply page challenges students to apply the measurement strategies to Grade 6 problems involving rates, percents, and common multiples. The Demonstrate page allows students to show what they have learned.

Note, the Explore, Practice, and Demonstrate pages can be used with students in earlier grades, even though the number-choices and problem-sequences were structured as a review or reteach for middle school students. In future posts, we will ask what the basic measurement strategy might look like in problems designed for grades 2-5.

Links to PDFs

Explore page

Practice page

Apply page

Demonstrate page

Why am I starting a blog about building fluency with a deep dive into number lines?
That’s a good question.

First, it’s a topic that offers up a “hmm, why did a student do that” moment with relatively little effort. The first post in this series focused on a basic number line problem, that when given to an academically diverse set of students in grades 3-8, will generate any number of incorrect answers. In addition, the justifications for the incorrect answers will reveal that a good number of students don’t understand the basic measurement concepts that govern number line representations. When I find problems that reveal a blatant and pervasive misconception with an important mathematical idea, it makes me want to dig deeper.

Second, number line representations show up everywhere we look in grades 3-12 math and beyond. Think about it: line plots, axes on a coordinate grid, double number lines, bar models, and continuous data representations all rely on students understanding how number lines work. In addition, number lines (axes) are fundamental to the study of algebra, geometry, trigonometry, calculus, and beyond. If a student doesn’t understand the basics of how number lines work, their academic career in math is likely to be shortened or significantly undermined.

Third, it’s a topic that teachers of many grade levels can appreciate. This blog is not targeted at any specific grade level band, even though many future topics will target a specific grade level range. To start things out, I tried to pick a topic that might interest a wide spectrum of math teachers and administrators.

Finally, I wanted a math topic that didn’t carry a lot of math-ed “baggage.” For example, had I picked whole number addition and subtraction, most of us would have started with very specific opinions. By choosing number lines, an important topic that carries very little controversy, we can nail down some areas of agreement before we tackle the “gloves are coming off” topics in math-ed.

So, let’s geek out on number lines with whole numbers!

Try This with Students

How do you think different students in your class would complete this number line?

How would students justify their placement of numbers on the line?

Extension Question: Where would students place 10 on the line and how would they justify their placement.

Well, go give it a try (a PDF version of the question is available below). Note, don’t do any instruction on number lines before giving this question to students. Let’s just see what they do with it and how they justify their number placement.

In addition, come up with a strategy for having students share their completed number lines and the reasoning behind their number placement. How you set this up will drive the quality of the classroom discussion. I have some ideas, but I’m interested in what folks out there come up with and where it leads their classroom conversation. (One thought, how could you use hypothetical student answers to start an argument?)

No matter how you have students share, be sure to take note of the justifications that students give, regardless of whether they get the problem wrong or right.

 

Let Us know What You Find

After you have a chance to do this problem with students, head over to the Comments Section for this post and let us know what students did and said.

 

Full Assessment –  Number Lines with Whole Numbers

The problem above is from an 8-question pre-assessment for a number line review unit designed for middle school students. This 4-lesson “mini” unit was designed to assess, and reteach where necessary, four number line concepts that are essential for success with middle school math representations (e.g. double number lines, bar models, axes on a coordinate grid, and many more). If you are interested in an assessment that will apply to a wider group of students, there is a link to the PDF of this 2-page assessment below.

Note, questions on this full assessment provide a conceptual roadmap for this series of Number Line blog posts. Since these other number line concepts will be addressed in future posts, let’s limit the discussion in the comments section to Problem 1 above.

Links to PDFs

Single problem per page (good for projecting on an LCD)

Multiple problems per page (waste less paper when making copies for students)

Full assessment (8 different problems on two pages)

Conjecture

Automaticity with a skill/strategy/concept in mathematics does not imply fluency with that skill/strategy/concept.

This blog will be about exploring this conjecture and trying to come up with a working definition of mathematical fluency that is meaningful and useful for a classroom teacher, parent, or math administrator.

That being said, I’m not going to spend a lot of time upfront trying to define fluency. Instead, I want to jump into doing some math with students. That is, I will offer up a set of problems that readers of this blog can do with students and then report back in the comments section on what students did. The goal is two fold:

• Introduce problems that challenge our understanding of how students think
• Provide a common context to explore what it means for a student to be fluent

So, let’s get started!